PROPRIEDADES DOS RADICAIS

A radiciação é uma operação matemática que envolve um produto (multiplicação) cujos fatores são todos iguais em seu fundamento, isto é, uma “potência”.

Enquanto que a potência, é um determinado número chamado de base, que é multiplicado por si mesmo n vezes (n é o expoente). Já radiciação, é feito o contrário: é dada a potência a fim de encontrar a base. 

Desse modo, tem-se as propriedades, conhecidas como propriedades dos radicais ou propriedades das raízes. Essas propriedades são utilizadas para simplificar e até mesmo para resolver raízes de índices elevados ou que possuam resultado não exato. Contudo, antes de uma exposição dessas propriedades, é bom relembrar o que é um radical e como encontrar seus resultados.

Para compreender melhor, vamos entender o que é um radical. Radical é o símbolo utilizado para identificar uma radiciação.

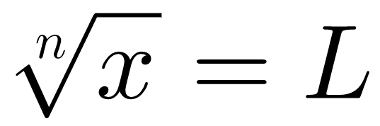
Definição da “raiz enésima de x”

Na imagem acima, n é o índice, x é o radicando e L é a raiz enésima. O símbolo “√” é conhecido como radical e é utilizado para representar a operação matemática radiciação. 

Sendo que, L é um número que, multiplicado por si mesmo n vezes, tem x como resultado, ou seja, Lⁿ = x. Dessa modo, a radiciação é o inverso da potenciação.

Então vamos lá !

Propriedades dos radicais ou propriedades das raízes

1ª Propriedade

A raiz enésima de um número elevado a enésima potência é o próprio número. Em outras palavras, essa propriedade trata das raízes em que o índice do radical é igual ao expoente do radicando. Observe:

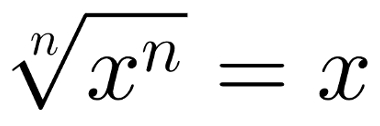
A raiz enésima de um número elevado a enésima potência

2ª Propriedade

O índice de uma raiz pode ser multiplicado (ou dividido) por um número real qualquer, desde que o expoente do radicando também seja multiplicado (ou dividido) pelo mesmo número. Matematicamente:

Multiplicação ou divisão do índice de um radical e do expoente do radicando pelo mesmo fator

3ª Propriedade

Essa propriedade trata das raízes em que o radicando é o produto entre dois números. Ela pode ser interpretada da seguinte maneira: A raiz enésima do produto é igual ao produto das raízes enésimas. Isso significa que:

A raiz do produto é igual ao produto das raízes

4ª Propriedade

Essa propriedade é idêntica à anterior, mas se aplica à divisão de dois números quaisquer. Nesse caso, a raiz enésima da razão é igual à razão entre as raízes enésimas. Observe:

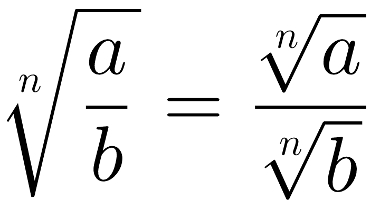
A raiz da razão é igual à razão das raízes

5ª Propriedade

Uma potência de uma raiz pode ser reescrita trazendo o expoente para o radicando. Matematicamente esta propriedade é dada da seguinte maneira:

Propriedade envolvendo uma potência de algum radical

6ª Propriedade

Essa propriedade diz respeito às raízes de raízes. Considerando a raiz enésima da raiz enésima de um número, é possível obter o seu resultado utilizando o seguinte:

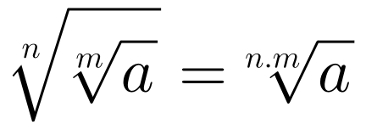
Propriedade envolvendo uma raiz de algum radical

7ª Propriedade

Todo radical pode ser escrito na forma de potência com expoente fracionário. Observe:

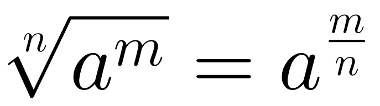
Propriedade que relaciona raízes de potências a potências com expoentes fracionários

Desse modo, as propriedades dos radicais permitem simplificar e resolver raízes de qualquer índice.