Alguns poliedros podem ser classificados em prismas ou pirâmides, de acordo com suas características.
Prismas são poliedros que possuem duas bases, que são polígonos iguais. Essas bases são ligadas por paralelogramos que chamamos faces laterais.
Veja o prisma de base pentagonal e sua planificação abaixo:
As pirâmides são poliedros que possuem uma única base e cujas faces laterais são formadas por triângulos.
Alguns elementos que podemos destacar em um prisma e em uma pirâmide são:
Note que o prisma de base triangular tem 6 vértices, 5 faces e 9 arestas.
Note, também, que a pirâmide de base quadrada tem 5 vértices, 5 faces e 8 arestas.
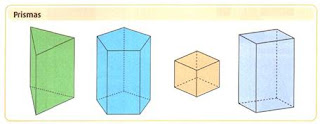
Os prismas podem ser classificados em retos ou oblíquos:
O prisma reto tem suas faces laterais formadas por retângulos.

O prisma oblíquo tem suas faces laterais formadas por paralelogramos.






13 comentários:
As três dimesões
A visualização no espaço
Em Matemática, a dimensão de um espaço é o número de parâmetros necessários para identificar um ponto desse espaço. Três dimensões significa termos três grandezas geométricas, largura, comprimento e profundidade. Muitas vezes, nós freqüentemente, abstraímos muitas figuras em 3 dimensões apenas observando sua representação plana, como na televisão, nos desenhos animados , nos filmes feitos em computação gráfica etc.
A Geometria Espacial (seja analítica ou sintética) é o ramo da Matemática que estuda as figuras nos espaço tridimensional.
Neste trabalho, vamos exercitar um pouco nossa abstração geométrica.
Sistema de Projeções (vistas)
Desenhar projeções é uma técnica de representação geométrica bidimensional para formas tridimensionais. É freqüentemente usada em Geometria descritiva e em Desenho técnico, para representar com precisão um determinado sólido.Projeção neste contexto, significa a representação na forma de imagem(foto, desenho) de determinada figura. Por exemplo, um mapa de sua cidade pode ter várias projeções distintas, cada uma adequada a cada tipo de propriedade a ser denotada. Ao construir um prédio por exemplo o é necessário calcular e definir cada peculiaridade da construção matematicamente, auxiliando na representação do problema geométrico envolvido.
A nossa sombra por exemplo é uma projeção da figura geométrica de nosso corpo. Observe se movimentamos uma lanterna, alterando a fonte luminosa, a sombra muda. Cada sombra representa uma diferente forma de projeção, se tivermos muitas projeções, podemos imaginar, ou mesmo determinar que tipo de figura espacial ela representa.
Obrigada pela contribuição!!!!
obrigado pela ajuda que vc esta mudado uma ajuda em mat
bem legale vai me ajudar em um trabalho do colégio
poderia ter as fórmulas para obter o volume, área, etc
mas estar muito bom.
Poderia acrescentar algumas formulas para calculo dos prismas. Ex. PIRAMIDE:
Uma piramide regular de base hesagonal tem 10cm de altura e a aresta da base mede 4 cm. Calcule
a)O apótema da base:
fórmula: l.V3
2
4.V3
2 = 2 V3 obs. V (rais quadrada)
área da base
fórmula: AB= 3l²v3
2
AB= 3.4²v3
2
AB= 3.16v3
2
AB= 48v3
2 = AB= 24v3cm
Esta muito interessante seu blog. Gostei Ass. Daniel Antunes
Muito bom ira me ajudar com meu trabalho de prismas e pirâmides
otimo mi ajuda mt seus gays travesti e.e
Muito bom este blog visite também http://quemfazmatematica.blogspot.com.br/
Olá Adriano,
Obrigada pela visita.
Fiz uma visita ao seu blog gostei muito....
Sucesso!!!!
gostei muito
Também acho que ficaria melhor com fórmulas.
Isabel - Professora de Matemática
muito bom!me ajudou no deveres!!!
Postar um comentário