MATRIZES
Como podemos notar nos exemplos 1, 2 e 3 respectivamente, uma matriz pode ser representada por colchetes, parênteses ou duas barras verticais.
- Definição: Matriz m x n é uma tabela de m . n números reais dispostos em m linhas (filas horizontais) e n colunas (filas verticais). Exemplos:
Como podemos notar nos exemplos 1, 2 e 3 respectivamente, uma matriz pode ser representada por colchetes, parênteses ou duas barras verticais.
2. Representação de uma matriz:
As matrizes costumam ser representadas por letras maiúsculas e seus elementos por letras minúsculas, acompanhadas de dois índices que indicam, respectivamente, a linha e a coluna ocupadas pelo elemento.
3. Matrizes especiais:
3.1 Matriz linha: É toda matriz do tipo 1 x n, isto é, com uma única linha.
3.2 Matriz coluna: É toda matriz do tipo n x 1, isto é, com uma única coluna.
3.3 Matriz quadrada: É toda matriz do tipo n x n, isto é, com o mesmo número de linhas e colunas. Neste caso, dizemos que a matriz é de ordem n.
Seja A uma matriz quadrada de ordem n.
Diagonal principal de uma matriz quadrada é o conjunto de elementos dessa matriz, tais que i = j.
Diagonal secundária de uma matriz quadrada é o conjunto de elementos dessa matriz, tais que i + j = n + 1..
Exemplo:
Descrição da matriz:
- O subscrito 3 indica a ordem da matriz;
- A diagonal principal é a diagonal formada pelos elementos –1, 0 e –6;
- A diagonal secundária é a diagonal formada pelos elementos 5, 0 e 5;
- a 11 = -1 é elemento da diagonal principal, pois i = j = 1;
- a 31 = 5 é elemento da diagonal secundária, pois i + j = n + 1 = 3 + 1.
3.4 Matriz nula: É toda matriz em que todos os elementos são nulos.
3.5 Matriz diagonal: É toda matriz quadrada onde só os elementos da diagonal principal são diferentes de zero.
3.6 Matriz identidade: É toda matriz quadrada onde todos os elementos que não estão na diagonal principal são nulos e os da diagonal principal são iguais a 1.
3.7 Matriz transposta: Chamamos de matriz transposta de uma matriz A a matriz que é obtida a partir de A, trocando-se ordenadamente suas linhas por colunas ou suas colunas por linhas.
3.8 Matriz simétrica: Uma matriz quadrada de ordem n é simétrica quando :
3.9 Matriz oposta: Chamamos de matriz oposta de uma matriz A a matriz que é obtida a partir de A, trocando-se o sinal de todas os seus elementos.
Notação: - A
3.10 Igualdade de matrizes: Duas matrizes, A e B, do mesmo tipo m x n, são iguais se, todos os elementos que ocupam a mesma posição são idênticos.
Notação: A = B.



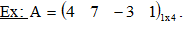












Nenhum comentário:
Postar um comentário